進階構造 (Advanced Constructions)
在本章中，將概述一系列非常強大的密碼學物件，即適用於任意電路（arbitrary circuits）的全同態加密（fully homomorphic encryption） 和基於屬性的加密（attribute-based encryption）。迄今為止，此類物件的唯一已知構造都是基於各種晶格問題（lattice problems）。在此，主要將注意力限制在基於 LWE 問題的構造上。

22.1 全同態加密 (Fully Homomorphic Encryption)
1978 年，Rivest、Adleman 和 Dertouzos [RAD78] 提出了一個後來被稱為全同態加密（Fully Homomorphic Encryption, FHE）的概念。（當時他們稱之為「隱私同態（privacy homomorphism）」）。簡而言之，一個 FHE 方案允許對加密數據進行計算，或者更簡潔地說，允許同態計算（homomorphic computation）：給定一個加密了某數據 μ 的密文（ciphertext），可以計算出一個加密了 f(μ) 的密文，其中 f 是任意所需的（可高效計算的）函數。強調，這是在完全不需要解密數據或知道解密金鑰的情況下實現的。

眾所周知，全同態加密在密碼學中具有豐富的應用，但在長達三十年的時間裡，沒有任何看似安全的方案被提出。這一情況在 2009 年發生了改變，當時 Gentry 基於理想格（ideal lattices）提出了一個候選 FHE 方案 [Gen09b, Gen09a]。Gentry 的開創性工作引起了巨大的轟動，並迅速催生了許多後續工作（例如 [vDGHV10, Gen10b, SV11, BV11a, CMNT11, BV11b, BGV12, CNT12, GHS12b, Bra12, GHPS12, CCK+13, GSW13] 等），這些工作在概念和技術的簡潔性、效率、安全性保證等方面提供了各種改進。在本節中，將概述基於 LWE 的近期 FHE 方案背後的主要思想，這些方案建立在前面章節描述的工具之上。更多細節，請參閱 Gentry [Gen10a] 和 Vaikuntanathan [Vai11] 的早期綜述。

22.1.1 基於 LWE 的 FHE (FHE from LWE)
最早的「第一代」FHE 構造 [Gen09b, vDGHV10] 分別基於關於理想格和「近似最大公因數（approximate GCD）」問題的特定（ad-hoc）平均情況假設。在一系列工作中，Brakerski 和 Vaikuntanathan（以下簡稱 BV）[BV11a, BV11b] 提出了「第二代」FHE 構造，這些構造基於具有最壞情況困難性（worst-case hardness）支持的標準假設，即（環-）LWE。在此描述 [BV11b] 中基於 LWE 的方案背後的主要思想，並附加其與 Gentry 後續工作 [BGV12] 中的一些改進。

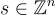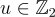BV 方案對每個密文加密一個單獨的位元 (bit)，並支持模二 (modulo two) 的同態加法 (addition) 和乘法 (multiplication)。儘管存在一些重要的注意事項（如下所述），但這對於 FHE 來說是足夠的，因為通過組合這些操作，可以同態地計算任何布林電路 (boolean circuit)。在 BV 系統中，秘密金鑰 (secret key) 是一個 LWE 秘密，而一個位元的加密僅僅是一個針對奇數模數 q 的 LWE 樣本 (sample)，其中誤差項 (error term) e 將訊息編碼為其最低有效位元 (least-significant bit)。更精確地說，在秘密金鑰 下加密 的密文是一個向量 使得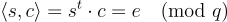

方程式 (22.1.1)
其中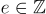 是某個小的誤差，滿足 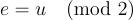，即 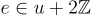要使用 s 解密 c，只需計算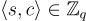

將結果提升 (lift) 到其在整數範圍內唯一的代表值 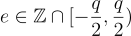，然後輸出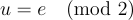
請注意，通過取 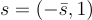密文向量 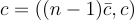，僅僅是一個具有 (n−1) 維秘密 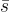和誤差項 e 的 LWE 樣本，因為 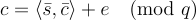在對稱金鑰設定 (symmetric-key setting) 中，這樣的密文可以直接使用 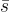產生；在非對稱金鑰設定 (asymmetric-key setting) 中，可以簡單地加上相對於 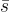的 LWE 樣本的隨機組合，這些樣本在公開金鑰 (public key) 中給出。（請注意，這本質上是所有基於 LWE 的公鑰加密 (LWE public-key encryption) 方案的工作方式）利用這些觀察，很容易證明密文是偽隨機的 (pseudorandom)，因此假設判定性 LWE (decision-LWE) 的困難性 (hardness)，該加密方案是被動安全 (passively secure) 的。

注意到，方程式 (22.1.1) 中表達的解密關係，即 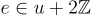有時被稱為訊息的「最低有效位元 (least significant bit)」編碼，以區別於貫穿第 5 章所使用的「最高有效位元 (most significant bit)」編碼，即 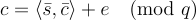。事實證明，當明文 (plaintext) 和密文模數 (ciphertext moduli) 互質 (coprime) 時，這兩種編碼是等價的，因為可以在不知道秘密金鑰的情況下輕鬆且無損地 (losslessly) 在它們之間切換。

同態操作 (Homomorphic operations):
現在描述同態加法和乘法。對於 i=1,2，令 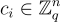為在秘密金鑰 s 下加密 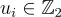的密文，具有小的誤差項 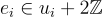同態加法很簡單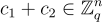： 加密了

因為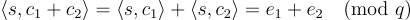

並且顯然 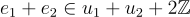仍然很小。然而，請注意不能無限制地添加密文，因為最終誤差的大小會增長到大於 q/2，在這種情況下解密可能會失敗。

同態乘法則有點棘手，從觀察開始：張量積（tensor）（或克羅內克積 Kronecker）乘積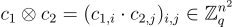

是在替代秘密金鑰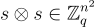
（即秘密金鑰與自身的張量積）下對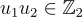
的有效加密。這是因為根據張量積的混合積性質（mixed-product property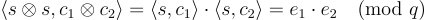）， 並且只要原始誤差足夠小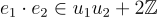， 仍然相當小。所以就像同態加法一樣，同態乘法的數量是先驗有界的（bounded a priori）。

金鑰切換 (Key switching):
上述的同態乘法有一個比誤差增長更顯著的問題：密文的維度（dimension）也增長得極快，即隨著（乘法次數）呈指數級增長（exponentially with the number of multiplied ciphertexts），這是由於使用了張量積（tensor product）。為了解決這個問題，BV 引入了一個巧妙的維度縮減（dimension reduction）技術 — — 也稱為金鑰切換（key switching）。假設有一個 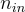維的密文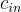

例如，如上所述的 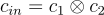它在秘密金鑰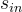

例如，如上所述的 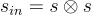下使用「最高有效位元（most-significant bit）」編碼加密了某個訊息 μ：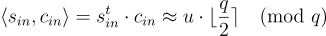

希望將 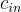轉換成一個 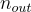維的密文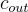
它仍然加密 μ，但是相對於某個可能不同的秘密金鑰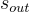

第一個主要的見解是：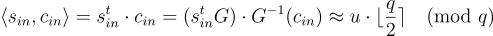

方程式 (18.1.2)

其中 G 是如第 18.2 中定義的具有 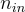行的 gadget 矩陣（gadget matrix）；同樣回想一下 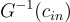是一個短的（short）整數向量。金鑰切換（key-switching）是通過發布一個在 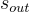下對 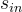的合適「加密」，即一個在 上的矩陣 K，使得以下等式成立來實現的：

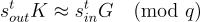
方程式 (18.1.3)
其中近似關係隱藏了小的誤差。本質上，K 的列是相對於 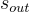的 LWE 樣本，並將 添加到最後一行。假設 LWE 的困難性（hardness），很容易證明這樣的 K 是偽隨機的（pseudorandom），因此只要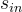
和 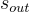是獨立的（independent），發布它是安全的。

要使用 K 對密文 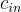進行金鑰切換，只需輸出 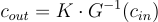將此與方程式 (18.1.2) 和 (18.1.3) 結合起來，可以看到：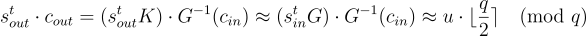

誤差管理與模數切換 (Error management and modulus switching):
回想一下，同態加法和乘法會增加結果密文中誤差項的大小；特別是，密文同態乘積中的誤差是各個誤差的乘積（由於金鑰切換，還會增加一點點）。這嚴重限制了方案的同態能力（homomorphic capacity）以及安全性/效率權衡（hardness/efficiency tradeoff）：模數 q 必須大於最終密文中的誤差，因此新加密的密文相對於 q 必須具有非常小的誤差率。更具體地說，到目前為止描述的方案只能同態地計算安全參數 λλ 中固定對數深度（logarithmic depth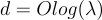） 的電路，因為模數必須是 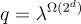，一個非常簡單但強大的模數縮減（modulus reduction）技術，首次在 [BV11] 中使用，然後在 [BGV12] 中發揮其全部潛力，極大地將同態能力擴展到安全參數中任何先驗有界的多項式深度（polynomial depth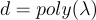） 的電路。其思想是，通過策略性地將模數縮小某個 poly(n) 因子（通常在進行同態乘法之前），可以將絕對誤差 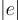減少到某個小的固定多項式大小，即使相對誤差率 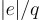。基本保持不變。因為絕對誤差是決定同態乘法中誤差增長的因素，模數縮減產生了一種套利（arbitrage），允許使用僅
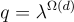的（原始）模數來計算深度為 d 的電路。更具體地說，在計算了電路的 d 層之後，的原始模數 q 縮減到 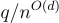而絕對誤差（absolute error）保持為 poly(n)。因此，將原始模數設置為 足以確保在深度為 d（depth-d）的計算後能夠正確解密（decryption）。

模數縮減技術依賴於 LWE 問題的正規形式 (normal form)，其中秘密 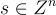是一個從誤差分佈中抽取的、相當短的整數向量（參見第 4.2.1 節）。主要思想是，將一個 LWE 樣本（具有短秘密）從
取整 到 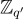會將絕對誤差縮放一個 q′/q 因子，再加上一個小的加法項: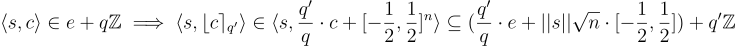

在全同態加密 (FHE) 的背景下，當密文採用最高有效位形式，即 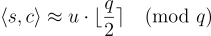時，可以驗證上述取整操作也保留了加密的消息。

還提到，Brakerski [Bra12] 給出了一種替代的「尺度不變 (scale invariant)」同態乘法方法，該方法僅將錯誤率增加一個固定的 poly(n) 因子，而與輸入密文的絕對誤差無關。使用這種方法，模數縮減變成可選的。然而，它仍然有用，因為隨著模數縮小，密文大小和計算時間也會變小。

參考資料
[RAD78] R. L. Rivest, L. Adleman, and M. L. Dertouzos. On data banks and privacy homomorphisms. Foundations of secure computation, 4(11):169–180, 1978.

[Gen09b] C. Gentry. Fully homomorphic encryption using ideal lattices. In STOC, pages 169–178. 2009.

[Gen09a] C. Gentry. A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University, 2009. http ://crypto.stanford.edu/craig

[vDGHV10] M. van Dijk, C. Gentry, S. Halevi, and V. Vaikuntanathan. Fully homomorphic encryption over the integers. In EUROCRYPT, pages 24–43. 2010.

[Gen10b] C. Gentry. Toward basing fully homomorphic encryption on worst-case hardness. In CRYPTO, pages 116–137. 2010.

[SV11] N. P. Smart and F. Vercauteren. Fully homomorphic SIMD operations. Designs, Codes and
Cryptography, 71(1):57–81, 2014. Preliminary version in ePrint Report 2011/133.

[BV11a] Z. Brakerski and V. Vaikuntanathan. Fully homomorphic encryption from ring-LWE and
security for key dependent messages. In CRYPTO, pages 505–524. 2011.

[CMNT11] J.-S. Coron, A. Mandal, D. Naccache, and M. Tibouchi. Fully homomorphic encryption over the integers with shorter public keys. In CRYPTO, pages 487–504. 2011.

[BV11b] Z. Brakerski and V. Vaikuntanathan. Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput., 43(2):831–871, 2014. Preliminary version in FOCS 2011.

[BGV12] Z. Brakerski, C. Gentry, and V. Vaikuntanathan. (Leveled) fully homomorphic encryption without bootstrapping. TOCT, 6(3):13, 2014. Preliminary version in ITCS 2012.

[CNT12] J.-S. Coron, D. Naccache, and M. Tibouchi. Public key compression and modulus switching for fully homomorphic encryption over the integers. In EUROCRYPT, pages 446–464. 2012.

[GHS12b] C. Gentry, S. Halevi, and N. P. Smart. Fully homomorphic encryption with polylog overhead. In EUROCRYPT, pages 465–482. 2012

[Bra12] Z. Brakerski. Fully homomorphic encryption without modulus switching from classical
GapSVP. In CRYPTO, pages 868–886. 2012.

[GHPS12] C. Gentry, S. Halevi, C. Peikert, and N. P. Smart. Field switching in BGV-style homomorphic
encryption. Journal of Computer Security, 21(5):663–684, 2013. Preliminary version in
SCN 2012.

[CCK+13] J. H. Cheon, J.-S. Coron, J. Kim, M. S. Lee, T. Lepoint, M. Tibouchi, and A. Yun. Batch fully
homomorphic encryption over the integers. In EUROCRYPT, pages 315–335. 2013.

[GSW13] C. Gentry, A. Sahai, and B. Waters. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In CRYPTO, pages 75–92. 2013.

[Vai11] V. Vaikuntanathan. Computing blindfolded: New developments in fully homomorphic encryption. In FOCS, pages 5–16. 2011.